LCM and HCF are the concepts that are used to find the greatest common divisors and least common multiples of two or more numbers.

The LCM of two or more numbers is the smallest number that is a multiple of each of the given numbers . It can be found by listing out the multiples of each number and finding the smallest multiple that each given numbers has in common.

The HCF of two or more numbers is the largest number that divides each of the given numbers. It can be found by listing the factors of each number and finding the largest factor that each number has in common.

In other words, HCF is the largest number that divides two or more numbers, while LCM is the smallest number that can be divided by two or more numbers.

Contents

Highest Common Factor (HCF) or Greatest Common Divisor (GCD)

HCF or GCD of two or more numbers is the greatest number that divides each of the numbers without leaving any remainder.

Different Method of Finding Highest Common Factor (HCF) or Greatest Common Divisor (GCD)

(i) HCF by Factorisation Method

Following steps must be followed:

Step 1. Find all the factors of each of the given numbers.

Step 2. Find their common factors.

Step 3. The largest of the common factors is the HCF of the given numbers.

Example : Find the HCF of 18, 24 and 30.

Solution: We have 18= 1 x 18; 18= 2 x 9; 18=3 x 6

24= 1 x 24 ; 24=2 x 12 ; 24= 3 x 8 ; 24= 4 x 6

30 = 1 x 30; 30= 2 x 15 ; 30=3 x 10; 30= 5 x 6

All the factors of 18 are: 1, 2, 3, 6, 9, 18

All the factors of 24 are: 1, 2, 3, 4,6,8,12, 24

All the factors of 30 are 1, 2, 3, 5,6 ,10, 15, 30

Common factors of 18 ,24 and 30 are : 1, 2, 3, 6

HCF of 18, 24 and 30 =6

(ii) HCF by Prime Factorisation Method

If a number is expressed in the form of product of prime numbers , then this form is called the prime factorisation of the given number .

Example : Find the HCF of 20, 28 and 36 by prime factorisation method.

Sol. Prime factorisation of 20, 28 and 36 are

The common factor of 20, 28 and 36 is 2(counting twice). Thus, HCF of 20, 28 and 36 is 2 × 2 = 4.

(iii) HCF by Long Division method

Step 1. Divide the bigger number by the smaller number.

Step 2. The remainder now becomes the new divisor and the previous divisor becomes the new dividend. Divide again.

Step 3. Continue till you get the remainder 0.

Example : Find the HCF of 35 and 49 by the long division method.

Sol.

HCF of 35 and 49

The HCF of 35 and 49 is 7

LCM (Lowest Common Multiple)

LCM of two or more numbers is the smallest multiple of each of the given numbers.

Different Method of Finding LCM (Least Common Multiple)

(i) To find LCM by finding common multiples of the given numbers

In this method , First write the some multiples of the given numbers, then find the common multiples of that numbers. The least multiple of the common multiples will be the LCM of the given numbers.

Example : Find the LCM of 4 and 6 .

Solution : The multiples of 4 = 4,8,12,16,20,24, 28 ………

The multiples of 6 = 6, 12, 18, 24, 30, ……………

Common multiples of 4 and 6 are 12, 24, ………

$\therefore$ the least common multiple of 4 and 6 is 12 .

Hence, the LCM of 4 and 6 = 12

(ii) LCM by Prime Factorization Method

To find LCM by prime factorisation method, steps are given below:

step 1 : Factorise each of the given numbers into product of prime factors.

Step 2: The LCM of the given numbers is the product of all different prime factors , taking the common prime factors occuring maximum number of times.

Example: Find the LCM of 90 , 108 and 144 by prime factorisation method.

Solution : Resolving each of the given numbers into prime factors , we get

90= 2 x 3 x 3 x 5 , 108= 2 x 2 x 3 x 3 x 3 144= 2 x 2 x 2 x 2 x 3 x 3

2 appears max. 4 times, 3 appears max. 3 times and 5 appears max. 1 time so, we take 2 four times, 3 three times and 5 one time and multiply to get the LCM.

$\therefore$ LCM of 90, 108 and 144 = 2 x 2 x 2 x 2 x 3 x 3 x 3 x 5 =2160

(iii) Short Division Method to find LCM

To find Least Common Multiple by using Division Method we need to follow the following steps.

step1 : Arrange the given numbers in a line .

Step 2: Divide them by a prime number, which exactly divides at least two of the given numbers and carry forward the numbers which are not divisible.

Step 3: Continue the process until all co-prime numbers are left in the last row.

Step 4: Now multiply all the prime numbers by which we have divided and the co-prime numbers left in the last row. This product is the least common multiple of the given numbers.

Example : Find the LCM of 12, 18, 24 and 36 by short division method .

Solution : we have

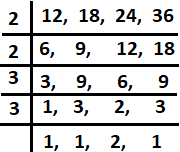
LCM = 2 x 2 x 3 x 3 x 2 = 72

Important facts about LCM and HCF

Two numbers are said to be co-prime , if their HCF is 1.
If one number is factor of other number, then smaller number is their HCF and larger number is their LCM.
The LCM of two co-prime numbers is equal to the their product.
Product of two given numbers is equal to the product of their HCF and LCM . Thus we have

$\mathrm{LCM \, of \, two\, numbers = \frac{First \, number \times Second \, \, number}{HCF \, of \, two\, numbers}}$

LCM and HCF of fractions

The formula to find HCF and LCM of fractions are given below :

$\mathrm{LCM \, of \, fractions =\frac{LCM \, of \, numerators}{ HCF \, of \, denominators} }$

$\mathrm{HCF \, of \, fractions =\frac{HCF \, of \, numerators}{ LCM \, of \, denominators}}$

Example : Find the LCM of $\frac{1}{3},\frac{1}{2},\frac{3}{7} \, \, and \, \, \frac{4}{11}$ .

Solution: LCM of the $\frac{1}{3},\frac{1}{2},\frac{3}{7} \, \, and \, \, \frac{4}{11}$ = $\frac{LCM \, of\, 1,1,3,4}{HCF \, of\, 3,2,7,11}$

= $\frac{12}{1}$

=12

Hence the LCM of the $\frac{1}{3},\frac{1}{2},\frac{3}{7} \, \, and \, \, \frac{4}{11}$ is 12 .

Example : Find the HCF of $\frac{4}{3}, \frac{4}{9}, \frac{2}{15} ,\frac{36}{21}$ .

Solution : HCF of $\frac{4}{3}, \frac{4}{9}, \frac{2}{15} ,\frac{36}{21}$ = $\mathrm{\frac{HCF \, of \, 4,4,2, 36}{ LCM \, of \, 3,9,15,21}}$

= $\frac{2}{ 315}$

LCM and HCF of decimal numbers

To find LCM and HCF of decimal numbers , the following steps should be followed:

Step I: Convert each of the decimals into like decimals by putting extra zeros on the right side of decimal point.

Step II: Now remove the decimal point and find the highest common factor and least common multiple of the obtained numbers as usual.

Step III: In the answer obtained in step 2, put the decimal point as there are number of decimal places in the like decimals.

Example :Find the LCM and HCF of 0.8 and 0.12.

Solution : Converting each of the decimals into like decimals , we get 0.80 and 0.12

Now, remove the decimal point and express each of the numbers as the product of primes we get

80= 2 x 2 x 2 x 2 x 5

12= 2 x 2 x 3

HCF of 80 and 12 is 2 x 2 =4

Therefore, the HCF of 0.80 and 0.12 = 0.04 (taking 2 decimal places)

LCM of 80 and 12 is = 2 x 2 x 2 x 2 x 3 x 5 = 240

Therefore, the LCM of 0.80 and 0.12 = 2.40 (taking 2 decimal places)

LCM and HCF practice Questions (Solved examples)

1. Find the LCM and HCF of 336 and 54 .

Solution: Factorise each of the given numbers into product of prime factors.

Prime factorisation of $336 = 2 \times 2 \times 2 \times 2 \times 3 \times 7$

Prime factorisation of $54 = 2 \times 3 \times 3 \times 3$

2 appears max. 4 times, 3 appears max. 3 times and 7 appears max. 1 time so, we take 2 four times, 3 three times and 7 one time and multiply to get the LCM.

Hence, LCM of $33 6 and 54 = 2 \times 3 \times 2 \times 2 \times 2 \times 7 \times 3 \times 3 = 3024$

Now for HCF ,The common factors of 336 and 54 are 2 and 3. Thus $H C F$ of $33 6 and 54 = 2 \times 3 = 6$

2. Find the LCM and HCF of 12, 15 and 21 .

Solution : Prime factorization of 12, 15 and 21 is

12=2×2×3

15=3×5

21=3×7

To find LCM we take all the factors present in three numbers and the highest power of the common factors respectively. Thus, L.C.M. of the given 3 numbers = 2 x 2 x3 x 7 x 5 =420

In all the three numbers, we can see that the number 3 is the common factors of all the given numbers. Hence, 3 is the HCF of the given three numbers.

Therefore, the required H.C.F. and L.C.M. of 12, 21 and 15 are 3, 420 respectively.

3. Find LCM and HCF of 510 and 92 .

Solution : 92 can be factorized as $2 \times 2 \times 23$ 510 can be factorized as $2 \times 3 \times 5 \times 17$

To find HCF, we take the lowest power of each of the common prime factors and to find LCM , we take the highest power of each of the prime factors.

Hence HCF = 2 and LCM = 2 x 2 x 3 x 5 x 17 x 23 = 23460

4. Given that HCF of 306 and 657 is 9, find LCM .

Solution : To solve this problem we use, $\mathrm{LCM \, of \, two\, numbers = \frac{First \, number \times Second \, \, number}{HCF \, of \, two\, numbers}}$

= $\frac{306 \times 657}{9}$

= $\frac{201042}{9}$

= 22,338

5. Find the HCF and LCM of $\frac{2}{3}, \frac{8}{9} , \frac{10}{27} \, \, and \, \, \frac{16}{81}$ .

Sol. we have $\mathrm{HCF= \frac{HCF \, \, of \, \, 2,8, 10, 16 }{LCM \, of\, \, 3, 9,27, 81 }}$

= $\frac{2}{81}$

$\mathrm{LCM= \frac{LCM \, \, of \, \, 2,8, 10, 16 }{HCF \, of\, \, 3, 9,27, 81 }} = \frac{80}{3}$

6. Two numbers are in the ratio 8:11 . If their HCF is 6 , find the numbers.

Solution : Let the numbers be $8x$ and $11x$ . Then their HCF = $x$

$\therefore x=6$

So, the numbers are $\left ( 8\times 6 \right ), \left ( 11\times 6 \right ) \, \, i. e. 48 \, \, and\, \, 66 .$

6. Find the largest number which can exactly divide 513, 783 and 1107 .

Solution: The largest number that can exactly divide 513, 783 and 1107 will be the HCF of 513, 783 and 1107 .

Prime factorisation of 513, 783 and 1107

513 = 3 x 3 x 3 x 19

783= 3 x 3 x 3 x 29

1107 = 3 x 3 x 3 x 41

So hcf of 513, 783 and 1107 is = 3 x 3 x3 = 27 .

Hence the required number is 27 .

7. Find the smallest number exactly divisible by each of the following of the numbers 12, 15, 20 , 27 .

Solution : Required number = LCM of 12, 15, 20 , 27

Finding LCM by short division method lcm of 12 15 20 27

Hence LCM = 2 x 2 x 3 x 3 x 3 x 5 = 240

8. Find the LCM of 3, 5, and 7.

Solution: Since LCM of co-prime numbers is equal to their product , So the LCM of 3, 5, and 7 is simply their product, which is 105.

9. Three friends have a certain number of candies. The first friend has 48 candies, the second friend has 60 candies, and the third friend has 72 candies. They want to divide the candies equally into small groups . What is the maximum number of candies in each group.

Solution: The maximum number of candies in each group will be the HCF of 48, 60 and 72 .

The factors of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24, and 48.

The factors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60.

The factors of 72 are 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, and 72.

Common factors of 48, 60 and 72 are = 1, 2, 3, 4, 6, 12

Hence the HCF of 48, 60 and 72 is 12 . So the maximum number of candies in each group is the HCF of these numbers, which is 12.

10. Find the greatest number which divides 148 and 100 leaving remainder 4 in each case .

Solution : Clearly , we have to find the largest number that divides (148-4) and (100-4) exactly. It means we have to find HCF of 144 and 96.

so required number = HCF of 144 and 96

=48

11. Five bells begin to toll together and toll respectively at intervals of 6,7,8, and 12 seconds. After how much time will they toll together again?

Solution : Required time = LCM of 6, 7, 8 and 12

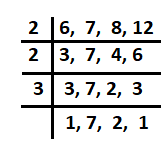
= 2 x 2 x 3 x 7 x 2

= 168 seconds =2 min. 48 sec

So, all the bell will toll together after 2 min. 48 sec.

Frequently Asked questions on LCM and HCF

Que: What is LCM and HCF?

Ans: LCM stands for “Least Common Multiple” and HCF stands for “Highest Common Factor”. LCM of two or more numbers is the smallest multiple of each of the given numbers, while the HCF of two or more numbers is the largest number that divides each of the given numbers.

Que : How can I find the LCM of two or more numbers?

Ans. To find the LCM of two or more numbers, you can list the multiples of each number and find the smallest multiple that they have in common. Another method is to find the LCM are prime factorization method and short division method.

Que: Can the LCM of two numbers be smaller than either of the two numbers?

Ans: No, the LCM of two numbers is always greater or equal to given numbers.

Que: What is the HCF of two prime numbers?

Ans: The HCF of two prime numbers is always 1, because prime numbers have no factors in common other than 1.

Que: Can the HCF of two numbers be greater than either of the two numbers?

Ans: No, the HCF of two numbers cannot be greater than either of the two numbers. HCF is always smaller or equal to the given numbers.

LCM and HCF worksheet PDF download

File Name: LCM-and-HCF-worksheet.pdf

You might also be interested in:

LCM and HCF | Different Method to Find LCM and HCF, Examples and Practice Questions

Highest Common Factor (HCF) or Greatest Common Divisor (GCD)

Different Method of Finding Highest Common Factor (HCF) or Greatest Common Divisor (GCD)

LCM (Lowest Common Multiple)