Area of Triangles: The area of a triangle or any plane figure is defined as the total space enclosed by their sides . Unit of measurement for area of any plane figure is taken as square metre () or square centimetre (
In this lesson, we will learn the different methods of finding area of triangles, along with some examples.
Different formula for finding area of a triangle:
Contents
Area of Triangles(General Formula)
The basic formula for finding the area of triangle is equal to half the product of its base and height. It is applicable to all types of triangles whether it is scalene, isosceles or equilateral.
| Area of triangle= |
When the triangle is right angled ( A triangle in which two sides are perpendicular ) , we can directly apply the formula by using two sides containing the right angle as base and height. For example, suppose that the sides of a right triangle ABC are 8 cm, 15 cm and 17 cm; we take base as 15 cm and height as 8 cm (see Fig. 2), then the area of triangle is given by
=
=60
Note : We could also take 8 cm as the base and 15 cm as height.
How to find area of triangle with 3 sides ?
Area of Scalene Triangle( Heron’s Formula)
A triangle whose all sides are different in length is called scalene triangle. Suppose we know the lengths of the sides of a scalene triangle and not the height. We can still find its area. Heron has derived the formula for the area of a triangle in terms of its three sides. The formula given by Heron about the area of a triangle, is also known as Heron’s formula. It is stated as:
| Area of a triangle = |
where ,
and
are the sides of the triangle and s= semi-perimeter i.e. half of the perimeter of the triangle=
.
This formula is helpful where it is not possible to find the height of the triangle easily.
Example : What is the area of the triangle whose sides are 8 m, 11 m, and 13 m.
Solution : We have cm
So,
Therefore , area of the triangle =
=
=
Area of triangle = .
How to find the area of an equilateral triangle?
Area of Equilateral triangle
Equilateral triangle is a triangle in which all the three sides are equal also all the three internal angles are equal. The formula for finding area of an equilateral triangle is
| Area of an equilateral triangle = |
Derivation for the formula of an equilateral triangle is given below.
Consider the following equilateral triangle ABC whose side length is ‘‘ units. Draw the altitude AD (the perpendicular segment from a vertex of a triangle to the opposite side ) . In an equilateral triangle all its altitude, angle bisector and median from any of its vertices are coincident (they are the same line segment). This can be proved using the concept of congruence of triangles. since AD is median to BC, BD=DC=
units.
Now AD is also the perpendicular to BC, we will use the Pythagorean theorem
() to determine its height AD= h units. In triangle ABD,
Area of =
=.
Example : Find the area of an equilateral triangle whose side is .
Sol. Area of an equilateral triangle =
=
=
Trigonometric formula for finding area of triangles ( Area of triangle with 2 sides and Included angle)
Consider the , whose vertex angles are ∠
, ∠
, and ∠
, and sides are
,
and
, as shown in the figure below.
 Now, if any two sides and the angle between them are given, then the formulas to calculate the area of a triangle is given by:
Now, if any two sides and the angle between them are given, then the formulas to calculate the area of a triangle is given by:
Since AD is perpendicular to BC, In
Substituting this value of in the formula Area=
, we get
.
This is also known as SAS formula for the area of a triangle. Similarly we can write the formula in terms of and
also.
Example: In ,
, side
units, side
= 8 units.
= =
)
Area = 12 square units.
Area of triangles formula using determinant
Let and
be the co Area of a triangle with vertices
and
is given by
Note: 1. Since area is a positive quantity , we always take the absolute value of the determinant in finding the area of triangle.
2. If area is given , use both positive and negative values of the determinant for calculation.
3. The area of triangle formed by three collinear points is zero.
Example: Find the area of the triangle whose vertices are (3,8), (-4, 2) and (5,1) .
Sol. Area of a triangle with vertices and
is given by
Putting the given values, area of the triangle is =
=
= sq. units
Area of triangles quizzes
Also read :
- Basic Trigonometric identities : < http://mathmitra.com/trigonometric-identities/ >
- Mensuration Formula for 2D and 3D shapes : <http://mathmitra.com/mensuration-formulas/>

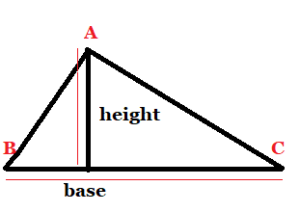 ( fig. 1)
( fig. 1) (fig. 2)
(fig. 2) 
