Class 8 Maths Chapter 1 (Rational numbers) Exercise 1.1
Class 8 maths chapter 1 exercise 1.2 solutions
NCERT maths class 8 chapter 1 (Exercise 1.2)
1. Represent these numbers on the number line. (i) (ii)
Sol. (i) To represent the number line may be divided into four equal parts as shown fig 1. We use the number
to name the first point of this division. The second point of division will be labelled
, the third point
, and so on . The point A will represent
.

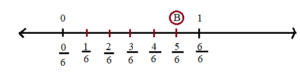
(ii) To represent the number line may be divided into six equal parts as shown fig 2. We use the number
to name the first point of this division. The second point of division will be labelled
, the third point
, and so on . The point B will represent
.
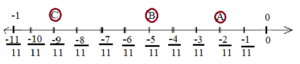
2. Represent on the number line.
Sol. Point A is , point B is
and point C is
.
3. Write five rational numbers which are smaller than 2.
Sol. Five rational numbers smaller than 2 are
4. Find ten rational numbers between .
Sol. We first convert to rational numbers with the same denominators.
and
Thus we have between
.
You can take any ten of these. In fact , you get countless rational numbers between any two given rational numbers.
5. Find five rational numbers between (i) (ii)
(iii)
Sol. (i) can be written as
and
as
.
Thus we have between
and
.
You can take any five of these.
(ii) can be written as
and
as
.
Thus we have between
and
.
You can take any five of these.
(iii) can be written as
and
as
.
Thus we have are five rational numbers between
and
.
6. Write five rational numbers greater than –2.
Sol. The five rational numbers greater than -2 are .
7. Find ten rational numbers between .
Sol. We first convert to rational numbers with the same denominators.
and
Thus we have between
.
You can take any ten of these. In fact , you get countless rational numbers between any two given rational numbers.
