Zeros of quadratic Polynomials

Geometrical interpretation  of zeros of quadratic  polynomials:

A polynomial of degree 2 is called a quadratic polynomial.  For any quadratic polynomial , ,

the graph of the corresponding equation     has one of the two shapes either open upwards like U or open   downwards like ,   ∩   depending on whether a > 0 or a < 0. (These curves are called parabolas.) 

The zeroes of a quadratic polynomial ,  are precisely the  x-coordinates of the points where the parabola representing intersects the x-axis.

Now the following three cases can happen.

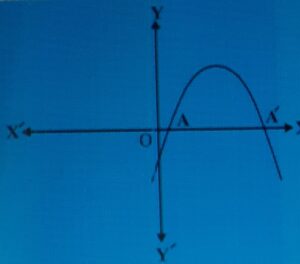
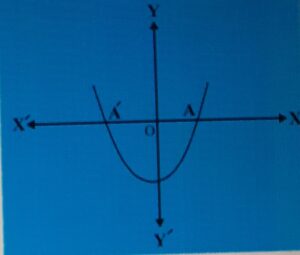
Case-(i)   The graph cuts x-axis at two distinct points. (See fig 1.) 

 

Fig. 1

   In this case , we get two distinct solutions  of y.

Case(ii)   The graph cuts the x-axis at exactly one point (see fig.2)

 

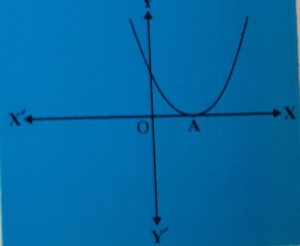
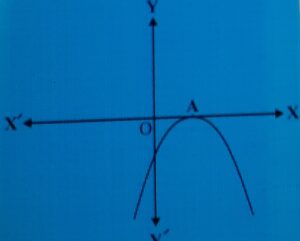
                                                              fig.(2)

The x-coordinate of A is the only zero for the quadratic polynomial in this case.

Case(iii) The graph is either completely above the x-axis or completely below  the x-axis.  (see Fig. 3).

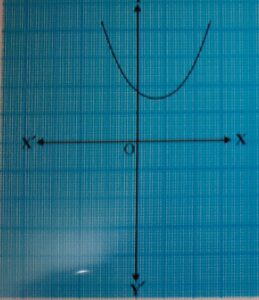
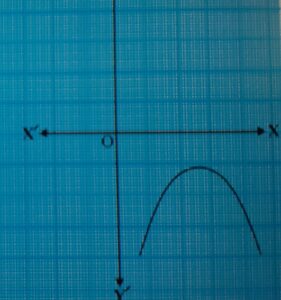
                                                          fig(3)

So, the quadratic polynomial has no zero in this case.

Thus we see  geometrically that a quadratic polynomial can have either two distinct zeroes or two equal zeroes (i.e., one zero), or no zero. This also means that a  polynomial of degree 2 has atmost two zeroes.