The Greatest integer function $f:\mathbb{R}\rightarrow \mathbb{R}$ is defined as $f(x)=\left \lfloor x \right \rfloor\, \, for \, \, \, all\, \, x\in \mathbb{R}$

, where $\left \lfloor \, \, \right \rfloor$ denotes the greatest integer that is less than or equal to $x$ .

In set notation we would write this as $\left \lfloor x \right \rfloor=max\left \{ m\in \mathbb{Z}|m\leq x \right \}$ . It is also called the floor function and step function.

Example. $\left \lfloor 3.7 \right \rfloor=3$ , $\left \lfloor - 2.3 \right \rfloor=-3$ and $\left \lfloor 4 \right \rfloor=4$

Domain and Range of Greatest integer function

Domain of greatest integer function is $\mathbb{R}$ ( the set of all real numbers) and range is $\mathbb{Z}$ ( the set of all integers ) as it only attains integer value.

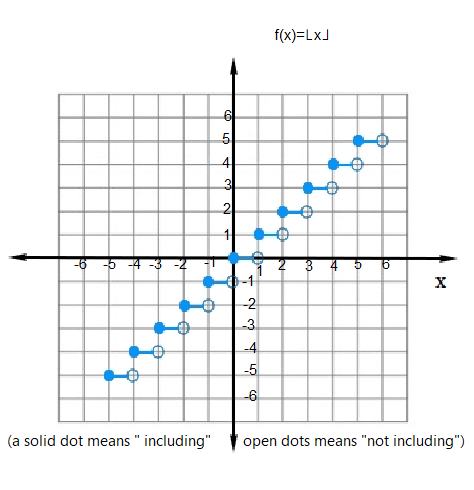
Graph of Greatest integer function

Let $f:\mathbb{R} \rightarrow \mathbb{R}$ be the greatest integer function define as

$y=\lfloor x \rfloor$ for all $x\in \mathbb{R}$

Let us calculate some value of $y$ for different value of $x$ .

$y=\lfloor x \rfloor =-1, \, \, \, -1\leq x <0$

$y=\lfloor x \rfloor =0, \, \, \, 0\leq x <1$

$y=\lfloor x \rfloor =1, \, \, \, 1\leq x <2$

$y=\lfloor x \rfloor =2, \, \, \, 2\leq x <3$

The graph of greatest integer function is given below.

Greatest integer function is neither one-one nor onto

A function $f$ from $A$ to $B$ is said to be one-one if whenever $f(a)=f(b)$ then $a=b$ . It means distinct elements have distinct image.

Here $f:\mathbb{R} \rightarrow \mathbb{R}$ is given by $f(x)=\left \lfloor x \right \rfloor$ ,

we can see that $f(1.3)=\left \lfloor 1.3 \right \rfloor=1$ and $f(1.7)=\left \lfloor 1.7 \right \rfloor=1$ .

$\therefore f(1.3)=f(1.7),$ but $1.3\neq 1.7$

Hence $f$ is not one-one.

A function $f$ from $A$ to $B$ is called onto if for all $b \in B$ there is an $a\in A$ such that $f(a)=b.$

Now consider $2.7 \in \mathbb{R}$ .

It is known that $f(x)=\left \lfloor x \right \rfloor$ is always an integer. Thus there does not exists any element $x\in \mathbb{R}$ such that $f(x)=2.7$ . Thus $f$ is not onto.

Hence , the Greatest integer function is neither one-one nor onto.

Continuity and differentiability of greatest integer function

Continuity and differentiability are properties of a function at a specific point rather than properties of a function as a whole . A function $f(x)$ is said to be continuous at a point c if each of the following condition is satisfied.

(i) $f(c)$ exists. (c is in the domain of $f$ )

(ii) $\lim_{x\rightarrow c}f(x)$ exists and

(iii) $\lim_{x\rightarrow c}f(x)=f(c)$

Geometrically, this means that there is no gap, split or missing point for $f(x)$ at $c$ and that a pencil could be moved along the graph of f(x) through $(c, f(c))$ without lifting it off the graph.

Greatest integer function is continous at all points apart from integral values of $x$ . It is also differentiable with ${f}'(x)=0$ , at all points apart from integral values of $x$ .

Let $c$ be an integer .Then we can find a sufficiently small real number $r>0$ such that $\left \lfloor c-r \right \rfloor=c-1$ whereas $\left \lfloor c+r \right \rfloor=c$ . Thus

$\lim_{x\rightarrow c^{-}}f(x)=\lim_{x\rightarrow c^{-}}\left \lfloor x \right \rfloor=c-1$ and $\lim_{x\rightarrow c^{+}}f(x)=\lim_{x\rightarrow c^{+}}\left \lfloor x \right \rfloor=c$ .

Since these limits cannot be equal to each other for any $c$ , the function is discontinous at every integral points.

The greatest integer function is continuous at evety real no. other than integers. For example

Let’s take x=1.5 . Then $\lim_{x\rightarrow 1.5^{-}}\left \lfloor x \right \rfloor=\lim_{x\rightarrow 1.5^{+}}\left \lfloor x \right \rfloor=1= \left \lfloor 1.5\right \rfloor$

In general, if $c$ is any number which is not an integer and $n-1<c<n$ , $n$ is an integer , then $\lim_{x\rightarrow c}\left \lfloor x \right \rfloor =n-1=\left \lfloor c \right \rfloor$ .