What are square roots ?

The process of multiplying a number by itself is called squaring. Finding the square root of a number is the inverse operation of squaring that number. For example the square of 3, 5 and 10 is 9, 25, 100 respectively.

Number	Square number
3	3×3=9
5	5×5=25
10	10×10=100

Numbers whose square roots are whole numbers are called perfect square numbers. For example 4,9 ,25, 36, 49 etc. are perfect square numbers . Numbers with decimal are not perfect square roots.

We have $3\times 3=9$ , therefore square root of 9 is 3. Also (-3)x (-3)=9 , we say that square root of 9 is 3 and -3. Thus all positive numbers have two square roots , one positive and one negative. Square roots of a number is denoted by the symbol $\sqrt{\, \, \, \, \, \, \, \, \, \, }$

Contents

Finding square root of perfect square number through prime factorisation

To find the square root of a perfect square number through prime factorisation the following steps must be followed:

Step -I: Factor the given number into the product of its prime factors.

Step-II: Make pair of similar factors.

Step-III: Take the product of prime factors , choosing one factor out of every pair.

Examples based on Prime factorisation method:

1. Find the square root of 7056.

Sol. Factor 7056 as a product of prime factors.

7056= $2\times 2\times 2\times 2\times 3\times 3\times 7\times 7$

Now making pairs of the prime factors of 7056

7056= 2 x 2 x 2 x 2 x 3 x 3 x 7 x 7

Take one factor from each pair and multiply them to find the square root of 7056.

$\sqrt{7056}= 2\times 2\times 3\times 7$ . Thus

$\sqrt{7056}= 84$

2. Is 9408 a perfect square? If not find the smallest multiple of 9408 which is a perfect square.Find the square root of the new number.

Sol. We have

9408= 2 x 2 x 2 x 2 x 2 x 2 x 3 x 7 x 7

As the prime factor 3 has no pair , 9408 is not a perfect square . If 3 gets a pair then number will become perfect square. So , we get multiply 9408 by 3 to get

9408 x 3 = 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3 x 7 x 7

Now each prime factor is in a pair .

Therefore 9408 x 3 = 28224 is a perfect square.

Thus the required smallest multiple of 9408 is 28224 which is a perfect square and

$\sqrt{28224} = 2\times 2\times 2\times 3\times 7$ =168.

Finding square root of a number through division method

When the numbers are large, the method of finding square root by prime factorisation
becomes lengthy and difficult. To overcome this problem we use Long Division Method. Let us understand the long division method with the help of an example.

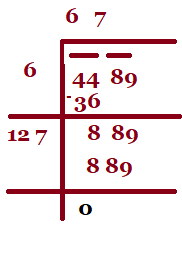
Example 1. Find the square root of 5476.

Sol. Step 1. Place a bar over every pair of digits starting from the digit at one’s place. If the
number of digits in it is odd, then the left-most single digit too will have a bar.

Step 2. Find the largest number whose square is less than or equal to the number under the
extreme left bar ( $7^{2}<54<8^{2}$ ). Take this number as the divisor and the quotient
with the number under the extreme left bar as the dividend (here 54). Divide and
get the remainder (5 in this case).

Step 3 . Bring down the number under the next bar (i.e., 76 in this case) to the right of
the remainder. So the new dividend is 576.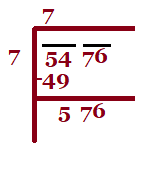

Step 4. Double the quotient and enter it with a blank on its right.

Step 5. Guess a largest possible digit to fill the blank which will also become the new
digit in the quotient, such that when the new divisor is multiplied to the new
quotient the product is less than or equal to the dividend.
In this case 144 × 3 = 432.
As 144 x 4 = 576, so we choose the new digit as 4. Get the remainder.