SAT Math Formula Sheet
You have probably never taken a math test like the SAT. It is intended to take known concepts and challenge you to use them in new ways. Although the test is challenging, you can raise your score by paying close attention to detail and being familiar with the fundamental formulas and concepts covered by the test. The SAT test includes a substantial amount of math. Your knowledge of the mathematical principles that you will need to study further in college is tested in this section of the exam. Heart of Algebra, Problem Solving and Data Analysis, and Passport to Advanced Math are the three main topics that this exam typically covers.
What equations must you therefore memorise before the exam date in order to pass the SAT math section? Every essential formula you MUST know before taking the test is covered in this helpful article.

SAT Math Formula Sheet
The Laws of Arithmetic
(a) The Commutative Law : According to the commutative law, no matter how we arrange the two numbers in an addition or multiplication operation, the final result will always have the same value. Or we may state that the outcome is unaffected by the sequence in which we add or multiply any two real numbers.
Hence, if a and b are two real numbers, then a+b =b+a and a.b =b.a
Note: Commutative law does not work for subtraction and division.
(c) The Distributive Law : According to the distributive law, if we multiply a number by a group of numbers that have been added or subtracted together, the result will be the same as if we multiple each number separately.
Example : (i)2 x (5+7) = (2 x 5) +(2 x 7)
(ii) 2 x (31- 24) = (2 x 31) -(2 x 24)
FOIL Method of multiplying two binomials:
When multiplying two binomials , you can use the shortcut called FOILing. For example,
F (multiply the first terms)
O (multiply the outside terms)
I (multiply the inside terms)
L (multiply the last terms)
Add all terms and simplify : =
Important Factoring Identities:
- If
Linear Equations :
(a) Slope-Intercept form :
(b) Standard form : slope =
y-intercept=
(c) Point -slope : slope =m point on line=
(d) Intercept form : x-intercept =a, y-intercept: = b
The Laws of equality :
To solve algebraic equations, you need the Laws of Equality.
(a) Whenever you do to change the value of one side of an equation , you must also do to the other side.
(b) You may add, subtract , or multiply anything you want on both sides of any equation at any time.
(c) You may divide both sides of any equation by any number except 0.
(d) If you want to take the square root of both sides of an equation , remember that every positive number has two square roots: one positive and one negative
Absolute value as Distance:
The absolute value of a number , written as |a| , is the distance from a to 0 on the number line, more generally , |a-b| means the distance between a and b on the number line, regardless of which number is greater.
The Laws of Inequality:
(a) Whatever you do to change the value of one side of an inequality, you must also do to the other side.
(b) You may add or subtract anything you want from both sides of an inequality, or multiply or divide by any positive number without changing the direction of the inequality.
(c) You may not perform undefined operations to an inequality.
(d) If you multiply or divide both sides by a negative number , you must switch the direction of the inequality. For example if x> 2 then -x<-2 .
System of Equations:
(a) Solving system by graphing: If a system of equations can be graphed , then the solution set is the intersection of their graphs. If the graphs are parallel lines , or any other non-intersecting graphs, then the system has no solution. If the graphs intersect multiple times, then the system has multiple solutions.
(b)Solving systems by substitution : If one variable is isolated in one of the equations of a system (or easy to isolate ), you can often solve the system by using Law of Substitution.
(c) The Law of Combination: If two equations are true , then you can add or subtract the corresponding sides of the equations together to get a new equation that is also true. This law allows you to combine equations in order to eliminate variables or to acquire expressions that a problem asks you to find.
The Average Formula:
The average of any set of numbers is calculated with the formula average =
or sum= average x number of numbers
Medians :
The median of a set of numbers is the number that divides the ordered set into two equal sets. That is , half the numbers are less than or equal to the median . To find the median of an ordered set of n numbers (increasing or decreasing ) ,
(i) Calculate .
(ii) If this is a whole number, then it is the “place” of the median. For instance, if there are 15 numbers in the set, then the median is the number in the set.
(iii) If this is not a whole number , then average the two numbers on either side of that “place”. For instance, if there are 16 numbers in the set , then , so the median is the average of the 8th and 9th numbers in the set.
Modes:
The mode of a set of numbers is the number that appears the most frequently. This means that not every number of set of numbers has a mode .
Percentages:
Commutativity of percentage : x% of y is the same as y% of x. For example , calculating 80% of 25 is a bit tricky, but it is easier if you think of it as 25% of 80, which is 20.
Changing by percentages: To increase a number by a% , just multiply by (100+a)% , and to decrease a number by a% , just multiply by (100 -a) %.
The percentage change formula: To find a percentage change , just use the formula
The Laws of Exponentials:
(i) If n is a positive integer, then means 1 times
repeatedly n times. If n is a negative integer , then
means 1 divide by x repeatedly |n| times.
(ii) If
(iii)
(iv)
(v)
(vi)
(vii)
(viii)
(ix)
(x) If , then a= b.
(xi) If , then
.
The Laws of Radicals :
(i)
(ii)
(iii)
The Intersecting Lines Theorem:
When two lines cross, the vertical angles are congruent and adjacent angles have a sum of 180°. 
The Parallel Lines Theorem:
When two parallel lines are crossed by a third line, they form either eight 90° angles or four acute angles and four obtuse angles, where all of the acute angles are congruent, all of the obtuse angles are congruent, and any acute angle is supplementary to any obtuse angle. 
The “ZCUF” Angles:
When a parallel lines diagram gets complicated, focus on the angle pairs that form any of the “ZCUF” angles, and memorize their relationships. But remember: these relationships apply only if the letters include two parallel lines. 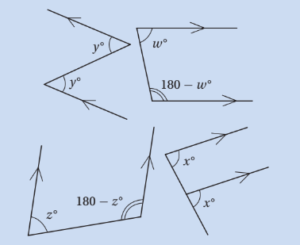
SAT Formulas related to the triangle:
(i) In any triangle, the sum of the interior angles is 180°.
(ii) Side-Angle Theorem: The biggest angle in a triangle is always across from the biggest side, and the smallest angle is always across from the smallest side. 
(iii) Isosceles Triangle Theorem: If two sides in a triangle are congruent, the two angles across from them are also congruent. Conversely, if two angles in a triangle are congruent, the two sides across from them are also congruent.
(iii) Exterior Angle Theorem : If we extend any side of a triangle, it makes an exterior angle with the adjacent side. The measure of any exterior angle is the sum of the two remote interior angles.
(iv) The Triangle Inequality: The sum of any two sides of a triangle must always be greater than the third side. This means that the length of any side of a triangle must be between the sum and the difference of the other two side lengths.

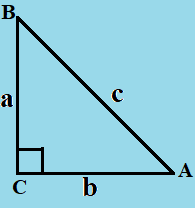
The Pythagorean Theorem: If a, b, and c are the lengths of the sides of a right triangle where c is the longest side, then
You might also be interested in:
- Area of Triangles
- Trigonometric values| Trigonometric ratio table
- List of Trigonometric Identities
- Mensuration Formulas for 2D and 3D Shapes PDF Download
- Factoring Polynomials Formula and Factoring Polynomials Worksheet with Answers
- Exponent formulas
- Percent formula
- Roman numbers : Chart and Rules

