Finding HCF is a fundamental concept of mathematics. For Class 6 students, grasping the idea of HCF is a crucial step in building a strong foundation in math. In this blog, we’ll explore HCF and provide some HCF questions to help you practice and understand it better.
Contents
What is the Highest Common Factor (HCF)?
The Highest Common Factor, or HCF, is the largest number that divides two or more numbers without leaving any remainder. It’s also known as the Greatest Common Divisor (GCD).
Why is HCF Important?
Understanding HCF is essential because it forms the basis for various mathematical concepts and real-life problem-solving situations. Here are a few reasons why HCF is important:
- Simplifying Fractions: Knowing the HCF of two numbers helps you simplify fractions. For instance, the HCF of 4 and 6 is 2, so you can simplify 4/6 to 2/3.
- Common Multiples: HCF is also useful in finding common multiples. It allows you to find the least common multiple (LCM), which is valuable in various mathematical operations.
- Word Problems: In everyday life, you might encounter scenarios where you need to divide something equally among a group of people. HCF helps you determine the largest group size without any leftovers.
Properties of HCF:
- The HCF of two or more numbers exactly divides the numbers.
- The HCF of given numbers can not be greater than the numbers themselves
- If one number is a factor of another number, the smaller number is the HCF.
- If the HCF of two numbers is 1, they are called co-prime numbers.
- Consecutive numbers are always co-prime. For example 7 and 8, 13 and 14 are co-prime numbers.
Lowest Common Multiple(LCM)
The lowest common multiple of two or more numbers is the smallest of their common multiples.
Properties of LCM :
- The LCM of two or more numbers is the smallest number that is completely divisible by each of the numbers.
- The LCM of two or more numbers can not be less than the numbers themselves.
- If one number is the factor of the other, the greatest number is the LCM.
- The LCM of co-prime is their product. For example LCM of 3 and 5 is 15.
Relation between HCF and LCM
| Product of two given numbers = product of their HCF and LCM |
HCF Questions for Class 6 (Solved examples)
Let’s practice with a few HCF questions to solidify our understanding:
(I)Find the HCF of 24 and 32 by Factorization method.
Sol. We have: 24=1 x 24 ; 24=2 x 12 ; 24= 3 x 8 and 24= 4 x 6
All the factors of 24 are : 1, 2 , 3, 4, 6, 8, 12, 24
Again , 32= 1 x 32; 32= 2 x 16; 32= 4 x 8
Common factors of 24 and 32 are : 1, 2, 4, 8
HCF of 24 and 32 is 8.
(II) Find the HCF of 72 and 90 by prime factorization method.
Sol. By prime factorization , we have : 72= 2 x 2 x 2 x 3 x 3 , 90= 2 x 3 x 3 x 5

HCF of 72 and 90 = product of common prime factors of 72 and 90
= 2 x 3 x 3
=18
Hence , the HCF of 72 and 90 is 18.
(III) Find the HCF of 135 and 180 by division method.
Sol.

HCF of 135 and 180 is 45 .
| HCF of three numbers = HCF of [( HCF of any two numbers) and the 3rd number] |
(IV) Find the HCF of 217 , 385 and 735 by division method.
Sol. First , we find the HCF of 217 and 385.
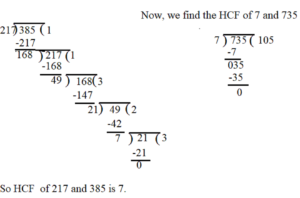
Clearly, 7 divides 735 completely, so the HCF of 7 and 735 is 7. Hence HCF of 217 , 385 and 735 is 7.
(V)Two buckets contain 15 litres and 25 litres of water. Find the maximum capacity of a mug that can exactly measure the water in both the buckets.
Sol. The maximum capacity of a mug will be the HCF of 15 and 25.
15= 3 x 5
25= 5 x 5
So, the HCF of 15 and 25 is 5.
Hence , the maximum capacity of a mug is 5 litres.
(VI)Two ropes, one 8 meters long and the other 12 meters long are to be cut into pieces of the same length. What will the maximum possible length of each piece be ?
Sol. The maximum possible length of each piece of rope of the same length that can be cut from the two given ropes is the HCF of 8 m and 12 m.
8 = 2 x 2 x 2
12 =2 x 2 x 3
So the HCF of 8 and 12 is 2 x 2 =4. (taking common factors only once)
Thus, the maximum possible length of each piece of rope is 4 m.
(VII) Find the greatest number which divides 148 and 100 leaving remainder 4 in each case.
Sol. Clearly, we have to find the largest number that divides (148-4) i.e. 140 and (100-4) i.e. 96 exactly.
Required number= HCF of 144 and 96
Prime factor of 144 and 96 are
144= 2 x 2 x 2 x 2 x 3 x 3
96= 2 x 2 x 2 x 2 x 2 x 3
HCF of 144 and 96= 2 x 2 x 2 x 2 x 3=48
Hence the required number is 48.
LCM questions for class 6
(VIII) Find the LCM of 90, 108 and 144 by prime factorization method.
Sol. Finding prime factors of each of the given numbers, we get :

90= 2 x 3 x 3 x 5 ; 108= 2 x 2 x 3 x 3 x 3 ; 144 = 2 x 2 x 2 x 2 x 3 x 3
The prime factor 2 appears maximum four times, the prime factor 3 appears maximum three times and the prime factor 5 appears maximum one time, so the required LCM is
LCM of 90, 108 and 144 = 2 x 2 x 2 x 2 x 3 x 3 x 3 x 5= 2160
(IX) Find the LCM and HCF of 680 and 816.
Sol. Prime factorisation of 680 and 816 are
680= 2 x 2 x 2 x 5 x 17
816=2 x 2 x 2 x 2 x 3 x 17
So, the HCF of 680 and 816 is = 2 x 2 x 2 x 17= 136
Now LCM =
=
So LCM= 4080
(X) Find the LCM of 96, 108 and 180 by short division method.
Sol.

LCM= 2 x 2 x 3 x 3 x 8 x 3 x 5 = 4320
(XI) Find the LCM of 40, 48 and 45 by prime factorisation.
Sol. The prime factorisation of 40, 48 and 45 are;
40 = 2 × 2 × 2 × 5
48 = 2 × 2 × 2 × 2 × 3
45 = 3 × 3 × 5
The prime factor 2 appears maximum number of four times in the prime factorization of 48, the prime factor 3 occurs maximum number of two times in the prime factorization of 45, The prime factor 5 appears one time in the prime factorisation of 40 and 45,
Therefore, required LCM = (2 × 2 × 2 × 2)×(3 × 3) × 5 = 720.
(XII) Find the least number which when divided by 12, 16, 24 and 36 leaves a remainder 7 in each case.
Sol. We first find the LCM of 12, 16, 24 and 36 as follows :

Thus, LCM = 2 × 2 × 2 × 2 × 3 × 3 = 144.
144 is the least number which when divided by the given numbers will leave remainder 0 in each case. But we need the least number that leaves remainder 7 in each case. Therefore, the required number is 7 more than 144.
Hence , the required least number = 144 + 7 = 151.
(XII) Two alarm clocks ring their alarms at regular intervals of 72 seconds and 50 seconds. If they beep together at noon, at what time will they beep again for the first time?
Solution: We find the LCM of 72 and 50.
Prime factorisation of 72 and 50,
Therefore, the LCM of 72 and 50 =
1800 seconds = 1800/60 min = 30 min
Hence, the clocks will beep again for the first time at 12:30 pm.
LCM and HCF questions for class 6 (Unsolved examples with answers)
(i) Find the HCF of the following numbers:
(a) 11, 44 (b) 35, 42 (c) 128, 60 (d) 81, 63 (e) 36, 180 (f) 1152, 1664
(ii) Find the HCF by finding all the factors.
(a)36, 48, 96 (b) 31, 37, 33 (c) 64, 74, 84
(iii) Find the HCF by prime factorisation.
(a)30, 45, 75 (b) 27, 30 (c) 18, 64, 80
(iv)Find the HCF by long division method.
(a)16 , 20 (b) 35, 95 (c) 65, 135
(v)Find the HCF of 70, 105, 175 .
(vi)Two buckets contain 15 litres and 25 litres of water. Find the maximum capacity of a mug that can exactly measure the water in both the buckets.
(vii)Two ropes, one 8 metres long and the other 12 metres long are to be cut into pieces of the same length. What will the maximum possible length of each piece be ?
(viii)The number of students of Std 6th and Std 7th who went to visit the Tadoba Tiger Project at Chandrapur was 140 and 196 respectively. The students of each class are to be divided into groups of the same number of students. Each group can have a paid guide. What is the maximum number of students there can be in each group ?
(ix)At the Rice Research Centre at Tumsar, there are 2610 kg of seeds of the basmati variety and 1980 kg of the Indrayani variety. If the maximum possible weight of seeds has to be filled to make bags of equal weight what should be the weight of each bag ? How many bags of each variety will there be ?
(x)Three pieces of timber 42m, 49m and 63m long have to be divided into planks of the same length. What is the greatest possible length of each plank?
Ans. (i) (a) 11 (b) 7 (c) 4 (d) 9 (e) 12 (f) 128 (ii) (a ) 12 (b) 1 (c) 2 (iii) (a) 15 (b) 3 ( c) 2 (iv ) (a) 4 (b) 5 (c )5 (v) 35 (vi) 5 litres (vii)4 m (viii)28 students (ix) maximum weight of each bag should be 90 kg, Number of bags filled with the seeds of basmati rice = 29 , Number of bags filled with the seeds of Indrayani rice= 22 (x)7m
LCM questions for class 6 (unsolved with answers)
(i) Find the LCM of 20, 30 and 50 by short division method.
(ii)Find the LCM of 96, 108 and 180 by short division method.
(iii) Find the LCM of 48 and 72 by prime factorization.
(iv)Four bells begin to toll together and toll respectively at intervals of 6, 7, 8 and 12 seconds. After how much time will they toll together again?
(v)What is the least number of children that can be arranged in rows of 10, 15 or 25 children in each row?
(vi)Find the LCM by the short division method.
(a) 30, 55 (b) 9 , 27 (c) 20, 65 (d) 10, 15, 25 (e)27, 54, 63
(vii)Find the LCM by prime factorisation method.
(a)24, 36 (b) 18, 27 (c) 40 , 32 (d) 21, 14, 42 (e) 10, 15, 18
(viii)Find the LCM of 12, 18, 24 and 36 by short division method.
(ix)Find the least number which is exactly divisible by each one of the numbers 12, 16 and 24.
(x) Find the least number of stones so that heaps of 15, 20 and 30 stones can be made.
Ans. (i) 300 (ii) 4320 (iii) 144 (iv) 2 min. 48 sec (v) 150 (vi) (a) 330 (b) 27 (c) 260 (d) 150 (e) 378 (vii) (a) 72 (b) 54 (c) 160 (d) 42 (e) 90 (viii) 72 (ix) 48 (x) 60
LCM and HCF questions for class 6 worksheet and PDF
You might also be interested in:
- BODMAS Questions grade 5
- Simplification grade 7
- Simplification questions for class 6 PDF
- Simplification tricks
- PEMDAS math rule
