November 19, 2024

Factoring trinomials worksheet

by Bina singhApril 17, 2022May 26, 2022

Factoring trinomials worksheet (solved examples)

Factorise the following Quadratic trinomials 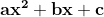$\mathbf{ax^{2}+bx+c}$ by spiliting the middle terms.

We know, in order to factorise the expression ax² + bx + c, we have to find two numbers p and q, such that p + q = b and p × q = ac.

Example 1: Factorise $\mathbf{x^{2}-7x+12}$

.

Solution. Find two factors p and q such that p+q=-7 and pq =12 . Take p=-3 and q=-4 then 12= -3 x (-4) and -3-4=-7 .

Therefore $\mathbf{x^{2}-7x+12}$ = $\mathbf{x^{2}+(-3-4)x+12}$

= $\mathbf{x^{2}-3x-4x +12}$

= $\mathbf{x(x-3)-4(x-3)}$

= $\mathbf{(x-3)(x-4)}$

Example 2: Obtain the factors of $\mathbf{x^{2}-4x-12}$

.

Solution. $\mathbf{x^{2}-4x-12}$ = $\mathbf{x^{2}-6x+2x-12}$

= $\boldsymbol{x(x-6)+2(x-6)}$

= $\mathbf{(x+2)(x-6)}$

Example 3: Find the factors of $\mathbf{3x^{2}+9x+6}$ .

Solution. Note that 3 is common factor in all the terms. Therefore

$\mathbf{3x^{2}+9x+6}$

= $\mathbf{3(x^{2}+3x+2)}$

= $\mathbf{3(x^{2}+2x+x+2)}$

= $\mathbf{3(x(x+2)+1(x+2))}$

= $\mathbf{3(x+1)(x+2)}$

Example 4: Factorise $\mathbf{x^{2}+5\sqrt{3}x+12}$ .

Solution. We split $5\sqrt{3}$

into two parts whose sum is $5\sqrt{3}$ and product is 12. Clearly $4\sqrt{3}+\sqrt{3}= 5\sqrt{3}$

and $4\sqrt{3}\times \sqrt{3}= 12$

$\therefore x^{2}+5\sqrt{3}x+12= x^{2}+4\sqrt{3}x+\sqrt{3}x+12$

= $x(x+4\sqrt{3})+\sqrt{3}(x+4\sqrt{3})$

= $(x+4\sqrt{3})(x+\sqrt{3})$

Hence $\mathbf{x^{2}+5\sqrt{3}x+12}$ = $(x+4\sqrt{3})(x+\sqrt{3})$

Example 5: Factorise $\mathbf{9x^{2}-22x+8}$ .

Sol. Here , 9 x 8 =72. We spilt -22 into parts whose sum is-22 and product 72 .

Clearly , (-18)+(-4) =-22 and (-18) x (-4)=72 .

$\therefore 9x^{2}-22x+8=9x^{2}-18x-4x+8$

= $9x(x-2)-4(x-2)$

= $(x-2)(9x-4)$

Hence $\mathbf{9x^{2}-22x+8}$ = $(x-2)(9x-4)$

Example 6: Factorise $\mathbf{6\sqrt{3}x^{2}-47x+5\sqrt{3}}$ .

Sol. Here , $6\sqrt{3}\times 5\sqrt{3}=90$

. We spilt -47 into two parts whose sum is-47 and product 90 .

Clearly , (-2)+(-45) =-47 and (-2) x (-45)=90 .

$6\sqrt{3}x^{2}-47x+5\sqrt{3}=6\sqrt{3}x^{2}-2x-45x+5\sqrt{3$

= $2x(3\sqrt{3}x-1)-5\sqrt{3}(3\sqrt{3}x-1)$

= $(2x-5\sqrt{3})(3\sqrt{3}x-1)$

Hence $\mathbf{6\sqrt{3}x^{2}-47x+5\sqrt{3}}$

= $(2x-5\sqrt{3})(3\sqrt{3}x-1)$ .

Example 7: Factorise $\frac{3}{5}x^{2}-\frac{19}{5}x +4$

.

Solution : Here, $\frac{3}{5} \times 4 = \frac{12}{5}$ . We split $-\frac{19}{5}$

into two parts whose sum is $-\frac{19}{5}$ and product $\frac{12}{5}$

.

Clearly, $-3-\frac{4}{5}=-\frac{19}{5}$ and $(-3)\times (-\frac{4}{5})=\frac{12}{5}$

.

$\frac{3}{5}x^{2}-\frac{19}{5}x +4$ = $\frac{3}{5}x^{2}-3x-\frac{4}{5}x +4$

= $3x(\frac{x}{5}-1)-4(\frac{x}{5}-1)$

= $(\frac{x}{5}-1)(3x-4)$

Hence $\frac{3}{5}x^{2}-\frac{19}{5}x +4$ = $(\frac{x}{5}-1)(3x-4)$

.

Example 8: Factorise $\boldsymbol{7\sqrt{2}x^{2}-10x-4\sqrt{2}}$ .

Solution: The given expression is $7\sqrt{2}x^{2}-10x-4\sqrt{2}$

.

Here , $7\sqrt{2}\times (-4\sqrt{2})=-56$ .

So, we split -10 in two parts whose sum is -10 and product -56.

Clearly, (-14+4) =-10 and (-14) x 4 =-56.

$\therefore$

$7\sqrt{2}x^{2}-10x-4\sqrt{2}$ = $7\sqrt{2}x^{2}-14x+4x-4\sqrt{2}$

= $7\sqrt{2}x(x- \sqrt{2})+4(x-\sqrt{2})$

= $(x-\sqrt{2})(7\sqrt{2}x+4)$

Factoring trinomials worksheet PDF download

PDF Loading...

You might also be interested in:

Bina singh

View all posts by Bina singh →

Leave a Reply Cancel reply