Here we have given the solutions of some important questions of chapter 1 (Set Theory) of NCERT Exemplar book .
Short answer type questions
1. Write the following sets in the roaster form
(i)
(ii)
(iii)
Sol. (i) On solving the equation , we get
Thus .
(ii) gives
which implies
Thus
(iii) Since every prime no. has only two factors 1 and number itself. This implies
2. Write the following sets in the roaster form:
(i)
(ii)
(iii)
Sol. (i) On solving , we get
, which implies either
or
.
Thus
(ii) implies
It gives .
Thus .
(iii) We have
This implies .
Therefore .
Q3. If . Write
in the roaster form.
sol. .
Since is prime number , it has only two factors 1 and (
) and the factors of
are 1,2,22,23,…,
. Therefore
.
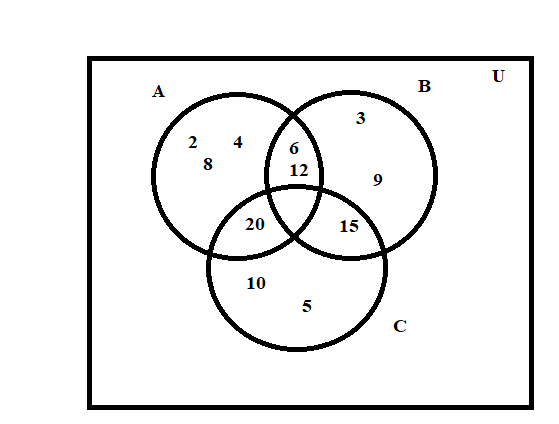
Q4. ,
and
are subsets of Universal Set
. If
and
is the set of all whole numbers, draw a Venn diagram showing the relation of
and
.
Sol. Here
Therefore ,
,
and
.
Hence, the Venn diagram showing relation of given sets is:
5. Determine whether the statement given below is true or false. Justify your answer.
For all sets ,
and
,
Solution: Let ,
then . This implies
…………..(i)
Now , this implies
…………..(ii)
From (i) and (ii) , it is clear that .
We can also show that the given expression is false by using Venn Diagrams
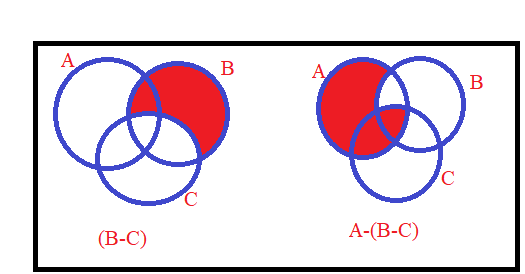
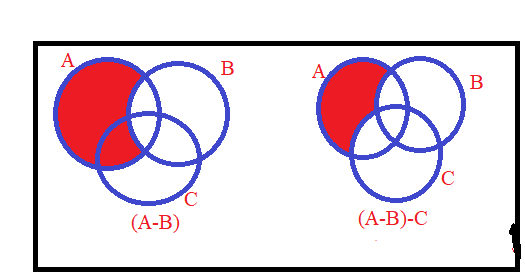
Now, from the Venn diagrams, it is clear that .

